Find the prime numbers that will divide n without the left over. Use Sieve of Eratosthenes to list all prime numbers smaller than n. Print all prime numbers in range, where a is less than b. Try to enlist all prime numbers smaller than the given one. Also, if you really like to create the faster solution, you could keep the numbers in some data structure that could outperform simple vector in this problem. One more idea is to create the list of prime numbers and search is the number in the list. That could sometimes catch the numbers that are not prime numbers. To benefit from this approach we could insert this before “ for” in the function. Also, there is one more trick, to generate accidental numbers and divide the candidate number with those numbers, but this way we will not get number that is prime for sure. The above approach is not bad for smaller numbers, but when the number that we are checking becomes to big it could slow down the program. Aldo, I am not sure is it possible to use just sqrt(n). The last potentially divisor is not greater than sqrt(n) +6. That way, those tests would be meaningless. 
We will have few tests that are not necessary but if one wishes it could find those numbers in the list of prime numbers that would be constructed. If they could be disassembled into composite numbers then those numbers will be of 6n+1 or 6n-1 form.
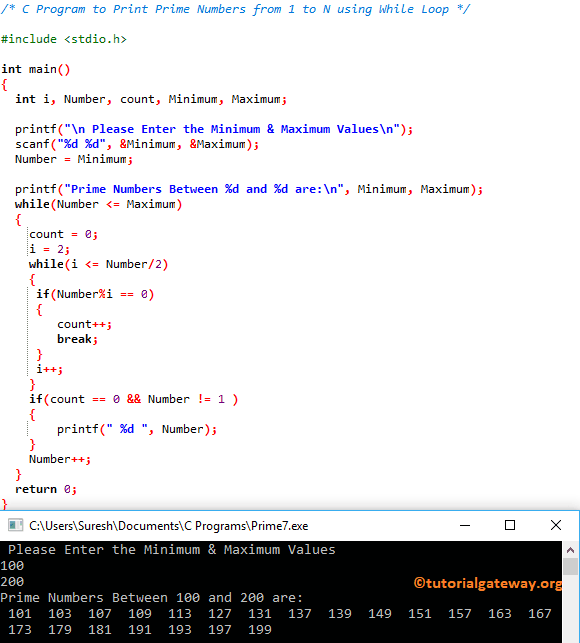
In the “for” we test all potentially prime numbers.
We divide the potentially prime number with 6, and if we get remain that is different than 5 or 1 we don’t have potentially prime number. Test if the number is: 2 or 3, because they are not of 6n+1 or 6n-1 form. If the logical function returns the true we print message that the number is prime, but if the function returns false we print the message that the number is not a prime number. If the respond is y or Y, we will test the next number with function IsPrime, otherwise we stop with the checking. We ask the user should we stop testing the numbers or should we continue with the testing. We create “do wile” circle that will enter the numbers to be examined. Write the header where we explain what we do in this program. If(!((iResidum = 5) || ( iResidum = 1))) return false įirst we will analyse the main function and then we will go in IsPrime() function. (IsPrime(myInput)=true)? cout<<"It is":cout<<"It is not" The following C++ example code will check whether the given number is a prime number or not. Last number that could be candidate to make tested number not prime, is not bigger than sqrt(n).Īlso one very important fact about prime number is that 1 is not prime number. But all numbers of 6n+1 or 6n-1 type are not prime numbers. All prime numbers are represented in that way, if they are bigger than 3.
0 kommentar(er)
